يعتبر الـ Recursion من المواضيع التي تبدو غير منطقية عند تعلمها لأول مرة فكيف نقوم باستخدام الFunction التي ما زلنا نحاول تعريفها ؟ هذا ما يجعل الـ Recursion معقداََ بعض الشئ بالنسبة لبعض المبتدئين. في هذا المقال سنحاول فهم الـ Recursion ولماذا يعمل كما سنقوم بشرح كيف يمكنك كتابة الـ Recursive Functions بنفسك.
فكرة الـ Recursion
الفكرة الأساسية للـ Recursion هي حل مشكلة كبيرة عن طريق تقسيمها إلى مشاكل أصغر منها -هذه المشاكل الأصغر تدعى Sub Problems- ، هذه الفكرة تظهر بشكل كبير في حياتنا اليومية فمثلاََ إذا أردت قراءة كتاب 500 صفحة فبدلاََ من قراءة كل الكتاب في يوم واحد تقوم كل يوم بقراءة 10 صفحات مثلاََ حتى تنتهي من الكتاب، في هذا المثال تقوم بنفس العملية – القراءة – ولكن على جزء صغير من الكتاب.
مثال آخر وهو إذا سألني شخص ما أن أجمع رقمين مثلاََ 25 + 58 فأقوم بالتفكير كالتالي:
- 50 + 20 = 70
- 8 + 5 = 13
- وبالتالي نتيجة الجمع تساوي 70 + 13 = 83.
في هذه الحالة لم أستطع جمع الرقمين مباشرةََ فقمت بتقسيم عملية الجمع الأصلية إلى عمليات جمع بين أرقام يسهل علىّ جمعها. يمكنك التفكير في أي مهمة كانت مطلوبة منك وقررت أن تقوم بتقسيمها إلى مهام أصغر منها وسيكون هذا مثال على الـ Recursion، وبالتالي الفكرة خلف الـ Recursion ليست بهذه الغرابة التي قد تبدو بها في البداية.
لماذا يعمل الـ Recursion ؟
عند تعلم الـ Recursion لأول مرة على الأرجح تظن أن هذا الكود غير صحيح وأنه سيسبب Error عند تنفيذه، في المثال التالي سنحاول فهم لماذا يعمل الـ Recursion.
في هذا المثال مطلوب أن نقوم بكتابة Function تأخذ عدد صحيح n وتقوم بحساب مجموع الأعداد الصحيحة من 1 حتى n، أمثلة على النتائج المطلوبة لقيم مختلفة لـ n:
- s(5) = 1 + 2 + 3 + 4 + 5 = 15
- s(8) = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36
والآن لنفكر في كيفية حل هذا السؤال باستخدام الـ Recursion، لنبدأ بالنظر إلى بعض الأمثلة:
- s(3) = 1 + 2 + 3 = 6
- s(4) = 1 + 2 + 3 + 4 = 10
- s(5) = 1 + 2 + 3 + 4 + 5 = 15
- s(6) = 1 + 2 + 3 + 4 + 5 + 6 = 21
هل تلاحظ نمط معين في هذه الأمثلة ؟ لننظر إلى المثال s(5) ،لحساب مجموع الأعداد الصحيحة من 1 حتى 5 نقوم بجمع الأعداد التالية: 1+2+3+4+5 إذاََ
s(5) = 1+2+3+4+5
والآن لننظر إلى (s(6 وفي هذه الحالة نقوم بجمع الأعداد 1+2+3+4+5+6 ولكننا نعلم أن 1 + 2 + 3 + 4 + 5 هو (5)s إذا يمكننا إزالة الأرقام 1 + 2 + 3 + 4 + 5 ووضع (5)s بدلاََ منهم وبالتالي يمكن أن نقول أن:
s(6) = 1+2+3+4+5 + 6
ولكن: s(5) = 1+2+3+4+5
اذاََ: s(6) = s(5) + 6
ويمكننا تعميم هذه العلاقة على جميع قيم n، بمعنى:
s(n) = s(n – 1) + n
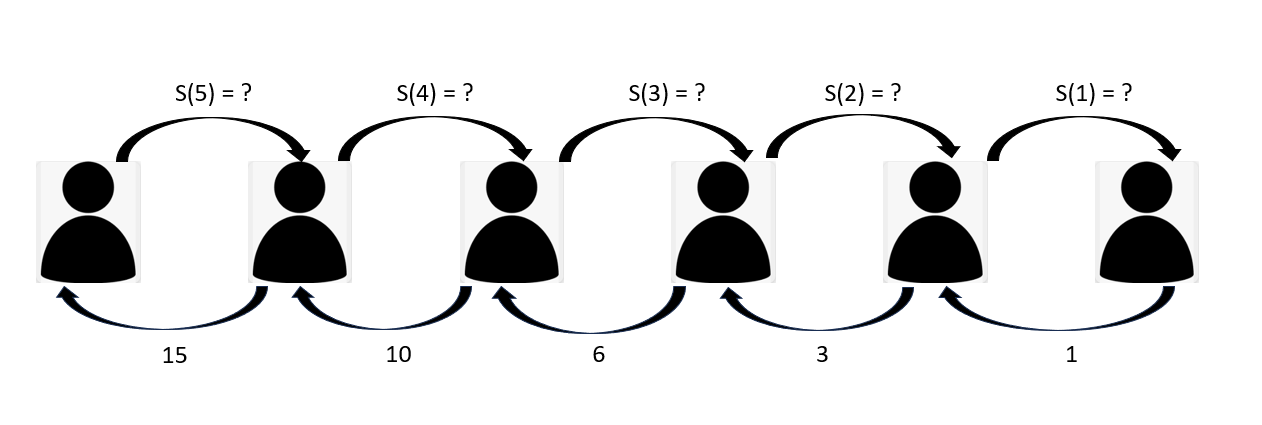
توضيح لهذه العلاقة لقيم مختلفة لـ n:
هذه المعادلة التي توصلنا إليها تخبرنا أنه لحساب مجموع الأعداد الصحيحة من 1 حتى n فيجب حساب مجموع الأعداد الصحيحة من 1 حتى n – 1 ثم جمع n على الرقم الناتج. لاحظ هنا أننا استخدمنا s(n – 1) لحل s(n) وهو تعريف الـ Recursion – حل مشكلة كبيرة عن طريق تقسيمها إلى مشاكل أصغر منها –
ولكن ما زال هناك مشكلة، لنحاول تطبيق المعادلة السابقة على n = 2:
لحساب s(2) نقوم بالتعويض في المعادلة وبالتالي s(2) = s(1) + 2، لحل هذه المعادلة نحتاج حساب قيمة s(1) ، لحساب s(1) نقوم بالتعويض في المعادلة مرة أخرى وبالتالي s(1) = s(0) + 1 والآن نحتاج حساب قيمة s(0)فنقوم بالتعويض في المعادلة مرة أخرى ولحساب قيمة s(0)سنحتاج حساب قيمة s(-1)وهكذا إلى ما لا نهاية، لحل هذه المشكلة نحتاج لشئ ما يجعلنا نتوقف عند قيمة معينة لـ n وهو ما يعرف بالـ Base Case، الـ Base Case هو الشرط الذي يجعل الـ Recursion يتوقف ويمنع الدالة من استدعاء نفسها دائماََ، الـ Base Case هو أبسط نسخة من المشكلة والتي يمكن حلها مباشرة دون الحاجة إلى تقسيم المشكلة إلى مشكلات أصغر.
في هذا السؤال أبسط input ممكن هو 1 في هذه الحالة المطلوب هو مجموع الأعداد الصحيحة من 1 وحتى 1 والذي يساوي 1، لا حاجة للـ Recursion في هذه الحالة.
والآن بعد إضافة الـ Base Case تم حل السؤال باستخدام الـ Recursion.
def s(n):
#base case
if n == 1:
return 1
#recursion
return s(n - 1) + nيمكنك مشاهدة كيف يعمل الكود عندما نقوم باستدعاء الـ Function وإعطائها قيمة n = 5:
يمكنك رؤية كيف تقوم s(5) باستدعاء s(4) ثم تقوم s(4) باستدعاء s(3) وهكذا حتى نصل إلى s(1) وهي الـ base case وفي هذه الحالة كل ما نقوم به هو 1 return.
وكل هذا يمنحنا فكرة عن لماذا يعمل الـ Recursion، الأمر أشبه بأن يطلب منك أحد أن تقوم بجمع الأعداد الصحيحة من 1 حتى 5 فتقوم بسؤال أحد أصدقائك عن مجموع الأعداد الصحيحة من 1 حتى 4 وصديقك بدوره يسأل أحد أصدقائه عن مجموع الأعداد الصحيحة من 1 حتى 3 وهكذا حتى نصل إلى الـ base case حينما يسأل شخص ما أحد أصدقائه عن مجموع الأعداد من 1 حتى 1 فيقوم صديقه بإخباره أن المجموع ببساطة يساوي 1
ومن هذه اللحظة كل شخص تم سؤاله قادر أن يحسب الناتج عن طريق القيام بعملية جمع وحيدة حتى يعود إليك صديقك ويخبرك أن مجموع الأعداد الصحيحة من 1 حتى 4 يساوي 10 فتقوم بجمع 5 على هذا الرقم وتجيب من سألك أن الناتج يساوي 15. لاحظ أن هناك مرحلتان، مرحلة حين يقوم كل شخص بسؤال صديقه باستمرار حتى نصل إلى السؤال الذي يمكن الإجابة عنه بسهولة ( base case ) ومرحلة حين يقوم كل شخص بالإجابة على من سأله حتى نصل إلى الناتج النهائي.
كتابة كود Recursive
هذه الطريقة في تتبع الـ Function calls بداية من الـ input الأصلي وصولاََ إلى الـ base case ثم تراكم الإجابات من الـ base case وحتى نصل إلى حل السؤال تجعلنا نفهم كيفية عمل الـ Recursion ولكنها قد لا تكون أفضل طريقة للتفكير عند التفكير في كتابة الكود الخاص بالـ Recursion، هذه مشكلة قد تواجه البعض عند محاولة حل الأسئلة باستخدام الـ Recursion وهي محاولة معرفة ما يحدث عند كل خطوة ولكننا في الواقع لا نحتاج الاهتمام بكل هذه التفاصيل عندما نقوم بالتفكير في حل لسؤال باستخدام الـ Recursion، لماذا ؟ سنشرح هذه الأفكار الآن من خلال مثال جديد مطلوب فيه كتابة Function تأخذ string وتقوم بعكسه، أمثلة:
- reverse(“hello”) -> “olleh”
- reverse(“eqraa”) -> “aarqe”
والآن لنفكر في كيفية الوصول لحل لهذا السؤال باستخدام الـ Recursion، على سبيل المثال لنفترض أن الـ string المعطى للـ Function هو hello، في البداية لنسأل أنفسنا كيف يمكن تصغير الـ input المعطى ؟ كيف يمكن جعل طول الـ string أصغر ؟ يمكن تحقيق ذلك عن طريق إزالة الحرف الأول بمعنى أنه يمكننا جعل الـ string المعطى -hello- أصغر عن طريق إزالة حرف h لنحصل على ello، لماذا نريد جعل الـ string المعطى أصغر ؟
تذكر أن فكرة الـ Recursion هي تقسيم المشكلة الأصلية إلى مشاكل أصغر منها (subproblems) والوصول لحل المشكلة الأصلية عن طريق حل هذه المشاكل الصغيرة. والآن لنسأل أنفسنا كيف يمكن استخدام حل المشكلة الأصغر للوصول إلى حل المشكلة الأكبر أو بمعنى آخر كيف يمكن استخدام عكس كلمة ello للوصول إلى عكس كلمة hello ؟
# reverse("hello") = "olleh"
# reverse("ello") = "olle"
# reverse("hello") = reverse("ello") + hيمكنك ملاحظة أنه لعكس كلمة hello نقوم بإزالة حرف الـ h لنحصل على ello ثم نقوم بعكس كلمة ello فنحصل على olle ثم نقوم بإضافة حرف الـ h في النهاية فنحصل على olleh وهو عكس كلمة hello، ويمكن تعميم هذه العلاقة لأي string تأخذه الدالة reverse:
reverse(s) = reverse(s[1:]) + s[0]
حيث s[1:] هو الـ string كله ما عدا الحرف الأول.
والآن كل ما يتبقى هو كتابة الـ base case، مرة أخرى لكتابة الـ base case نفكر في أبسط string يمكن أن يدخل إلى الدالة، إذا كان الـ string فارغ أو عبارة عن حرف وحيد فلا نحتاج للقيام بأي عمل إضافي لعكسه فقط نقوم بعمل return لهذا الـ string.
def reverse(s):
if len(s) <= 1:
return s
return reverse(s[1:]) + s[0]توضيح لكيفية عمل الكود:
لنراجع الخطوات التي قمنا بها لحل هذا السؤال، المطلوب كان كتابة دالة تقوم بعكس string وقمنا باتباع هذه الخطوات:
1- سألنا أنفسنا كيف يمكن جعل الـ string أصغر وتوصلنا أن هذا ممكن من خلال إزالة الحرف الأول
2- سألنا أنفسنا كيف يمكن استخدام عكس الـ string الأصغر للوصول إلى عكس الـ string الأصلي وإجابة هذا السؤال كانت إضافة الحرف الأول من الـ string الأصلي إلى عكس الـ string الأصغر
3- قمنا بتحديد الـ base case
لاحظ هنا في الخطوة الثانية سألنا كيف يمكن استخدام عكس الـ string الأصغر للوصول إلى عكس الـ string الأصلي ولم نهتم كيف سيتم عكس الـ string الأصغر، فقط افترضنا أنه يمكن عكس الـ string الأصغر ثم بدأنا في التفكير في كيفية استخدام ذلك للوصول إلى عكس الـ string الأصلى.
هذا ما كنت أقصده عندما قلت أننا لا نحتاج للاهتمام بتفاصيل عمل الـ Recursion عند كتابة الكود، عند كتابة الكود لا نهتم كيف سيعمل الـ Recursion على أي input أصغر من الـ input الأصلي ( subproblrm) ، فقط نفترض أن الـ Function التي نقوم بكتابتها الآن تعمل بالفعل على أي input أصغر من الـ input الأصلي ثم نفكر كيف يمكن استخدام ذلك لحل السؤال.
هذا المبدأ يعرف بـ The Recursive leap of faith
The Recursive leap of faith
هذا المبدأ يعني أننا نفترض أن الدالة التي نقوم بكتابتها الآن تعمل بالفعل على أي input أصغر من الـ input الأصلي أو على أي subproblem، بمعنى أنه إذا كنا نكتب دالة لعكس string طوله N فإننا نفترض أن هذه الدالة يمكنها عكس أي string طوله أقل من N، هذا المبدأ يبدو غير منطقي فكيف نفترض أن الدالة التي لم نكتبها بعد تعمل بالفعل ؟
ولكننا رأينا كيف يعمل الـ Recursion أثناء هذا المقال، رأينا في المثالين السابقين كيف تقوم كل دالة باستدعاء نفسها على input أصغر منها حتى نصل إلى الـ base case وبالتالي عند استدعاء الدالة على input أصغر من الـ input الأصلي يمكننا تتبع هذه الخطوات لنرى أنه سوف يعمل في النهاية ولكن الـ Recursive leap of faith يخبرنا أن نختصر هذه الخطوات، لا تتبع الـ Recursion على أي subproblem ولكن افترض أنه سيعمل وسيعطيك النتيجة الصحيحة لهذه الـ subproblem.
وبالتالي العقلية التي يجب أن نمتلكها عند كتابة كود Recursive ليست كيف تعمل الدالة على كل input ولكن إذا كانت الدالة تعمل بالفعل على الـ subproblem كيف يمكن استخدام ذلك لحل السؤال الأصلي ؟
Declarative vs imperative programming
قد تبدو فكرة غريبة أننا نقوم باستدعاء دالة دون الاهتمام بتفاصيل تنفيذها ونهتم فقط بنتيجة استدعاء هذه الدالة، ولكن هذه طريقة عامة لكتابة الكود تسمى declarative programming، بشكل عام هناك طريقتين لكتابة الكود الأولى تسمى imperative programming والتي تهتم بكيفية عمل البرنامج وفيها نقوم بإخبار الكود بتعليمات تصف بالضبط كيف يجب أن يعمل البرنامج.
على العكس declarative programming تهتم بالوظيفة التي يجب أن يؤديها البرنامج دون الاهتمام بكيفية القيام بهذه الوظيفة، لنشرح الفرق من خلال مثال إذا كان لدينا array به أرقام ونريد أن نختار الأرقام الزوجية فقط من هذا الـ array ، إذا قمنا بكتابة هذا الكود بطريقة imperative ستكون كالتالي:
arr = [1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10]
even_numbers = []
for i in range(len(arr)):
if arr[i] % 2 == 0:
even_numbers.append(arr[i])لكتابة نفس الكود بطريقة declarative:
arr = [1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10]
even_numbers = list(filter(lambda x : x % 2 == 0 , arr))في الكود الـ imperative قمنا بتحديد الخطوات اللازمة لاختيار الأرقام الزوجية فقط من الـ array، بينما في الكود الـ declarative قمنا باستدعاء الدالة filter للقيام بنفس الوظيفة.
الـ Recursion يعتمد على الطريقة الـ declarative في كتابة الكود والتي تركز فقط على الوظيفة التي يقوم بها البرنامج وليست الطريقة التي يؤدي بها تلك الوظيفة، هذا يشبه استخدام مكتبة في الكود الخاص بك فأنت تقوم باستدعاء الدوال التي توفرها لك هذه المكتبة مهتماََ فقط بالوظيفة التي تقوم بها الدالة دون التفكير في كيفية قيامها بهذه الوظيفة. لذلك عند كتابة كود Recursion يجب على المبرمج أن يفكر فقط في الوظيفة التي تقوم بها الدالة وأن يفترض أن الدالة تؤدي هذه الوظيفة بنجاح على أي input أصغر من الـ input الأصلي أو أي subproblem. التفكير في التفاصيل الصغيرة وتتتبع الـ Recursion حتى الوصول إلى الـ base case غالباََ ما يؤدي للارتباك.
والآن لننظر إلى مزيد من الأمثلة
IsPalindrome
مطلوب في هذا المثال دالة تأخذ string وتقوم بتحديد إذا كان palindrome أم لا، الـ string يكون palindrome عندما يكون نفس الـ string عند قراءته من اليسار لليمين ومن اليمين لليسار أمثلة:
- isPalindrome(“aaabaaa”) -> True
- isPalindrome(“baa”) -> False
- isPalindrome(“aa”) -> True
لنبدأ بالخطوة الأولى، كيف يمكن جعل الـ input أصغر ؟ من تعريف الـ palindrome أنها نفس الكلمة يمكن قراءتها من اليسار لليمين أو من اليمين لليسار أو بمعنى آخر يمكن قراءتها من البداية للنهاية أو العكس، يمكننا أن نبدأ بمقارنة أول حرف وآخر حرف في الكلمة، إن لم يكونوا متساويين إذا هذه الكلمة ليست palindrome ولكن إن كانوا متساويين فهناك احتمال أن تكون الكلمة palindrome وبالتالي يجب أن ننظر إلى باقي الحروف باستثناء الحرف الأول والأخير لنتأكد من ذلك، إذا الخطوة الأولى هي أننا سنجعل الكلمة أصغر عن طريق إزالة الحرف الأول والأخير إن كانا متساويين.
الخطوة التالية ستكون أن ننظر إلى ما تبقى من الكلمة بعد إزالة الحرفين الأول والأخير ونفكر كيف يمكن استخدام نتيجة استدعاء الدالة isPalindrome على ما تبقى من الكلمة لتحديد إذا كانت الكلمة الأصلية palindrome أم لا. عند استدعاء الدالة isPalindrome على ما تبقى من الكلمة بعد ازالة الحرفين الأول والأخير النتيجة ستكون True أو False بناءاََ على إذا ما كان هذا الجزء palindrome أم لا، إذا كان palindrome إذاََ الـ string الأصلي palindrome والعكس. ملخص ما وصلنا إليه حتى الآن هو أن الـ string يكون palindrome عندما يتحقق الشرطين التاليين:
- الحرف الأول والأخير متساويين
- ما يتبقى من الـ string بعد إزالة الحرفين الأول والأخير يكون palindrome
توضيح لهذين الشرطين على كلمات مختلفة:
كل ما يتبقى الآن هو الـ base case، أبسط input لهذه الدالة هو string فارغ أو به حرف وحيد وفي هذه الحالة يعتبر palindrome لذلك نقوم عمل return لـ True.
def isPalindrome(s):
if len(s) <= 1:
return True
return s[0] == s[-1] and isPalindrome(s[1:-1])توضيح لكيفية عمل الكود:
Climbing Stairs
في هذا المثال هناك سلم مكون من عدد n درجة ونحن نريد الصعود إلى قمته وفي كل خطوة يمكننا صعود درجة أو درجتين لأعلى والمطلوب هو عدد الطرق التي يمكن بها الصعود إلى قمة السلم. أمثلة:
climbStairs(2) = 2
climbStairs(3) = 3
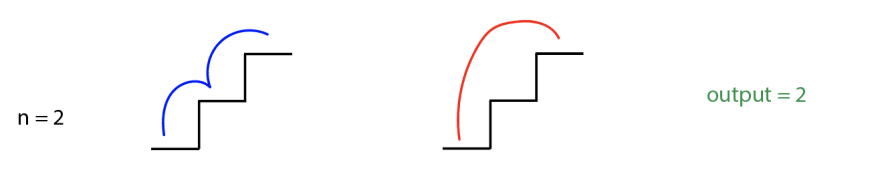


مصدر الصور:
مرة أخرى، الخطوة الأولى هي كيف نجعل الـ input أصغر؟ لدينا سلم عدد درجاته n ما الذي يمكننا فعله لجعل عدد الدرجات أصغر؟ السؤال يخبرنا أننا لدينا اختيارين:
1- الخيار الأول هو صعود درجة لأعلى في هذه الحالة يتبقى n – 1 درجة للوصول إلى قمة السلم
– الخيار الثاني هو صعود درجتين لأعلى في هذه الحالة يتبقى n – 2 درجة للوصول إلى قمة السلم
الخطوة التالية هي كيف سنقوم باستخدام نتيجة استدعاء الدالة على n – 1 و n – 2 لحساب عدد طرق صعود سلم عدد درجاته n.
كما ذكرنا سابقاََ أنه في كل خطوة لدينا خيارين إما صعود درجة أو درجتين، إذا قررنا في البداية أن نقوم بصعود درجة واحدة سيتبقى n -1 درجة، استدعاء الدالة climbingStairs وإعطائها input = n – 1 يعطينا عدد الطرق لصعود هذه الدرجات المتبقية. وإذا قررنا في البداية أن نقوم بصعود درجتين سيتبقى n – 2 درجة، استدعاء الدالة climbingStairs وإعطائها input = n – 2 يعطينا عدد الطرق لصعود هذه الدرجات. لتغطية جميع الاحتمالات سنقوم بجمع ناتج استدعاء الدالة climbingStairs عند إعطائها n – 1 على ناتج استدعاء الدالة climbingStairs عند إعطائها n – 2.
climbStairs(n) = climbStairs(n – 1) + climbStairs(n – 2)
بالنسبة للـ base case هناك حالتين:
1- إذا كان السلم عبارة عن درجة واحدة فلا يوجد سوى طريقة واحدة للوصول لقمة هذا السلم وهي صعود هذه الدرجة.
2- إذا كانت n = 0 هذا يعني أنه لا يوجد درجات في هذا السلم وبالتالي هناك طريقة وحيدة لصعود هذا السلم وهي ألا نقوم بأي شئ على الإطلاق.
باختصار ما قمنا به لحل هذا السؤال هو التالي:
1- نظرنا إلى الاختيارات المتاحة في كل خطوة وهما خياران إما صعود درجة أو درجتين
2- عند صعود درجة يصبح عدد درجات السلم المتبقية n – 1، عدد طرق صعود هذه الدرجات هو climbStairs(n – 1)
3- عند صعود درجتين يصبح عدد درجات السلم المتبقية n – 2، عدد طرق صعود هذه الدرجات هو climbStairs(n – 2)
4- للحصول على عدد طرق صعود سلم عدد درجاته n يتم جمع عدد طرق الصعود الناتجة من تنفيذ الاختيار الأول – صعود درجة – وهو climbStairs(n – 1) على عدد طرق الصعود الناتجة من تنفيذ الاختيار الثاني – صعود درجتين – وهو climbStairs(n – 2)
5- قمنا بتحديد الـ base case وهو عندما n = 0 أو n = 1 وفي الحالتين الحل هو أن هناك طريقة واحدة.
def climbStairs(n):
if n <= 1:
return 1
return climbStairs(n - 1) + climbStairs(n - 2)توضيح لكيفية عمل الكود عند n = 4
في الختام
خلال هذا المقال رأينا الفكرة الأساسية للـ Recursion ورأينا كيف يعمل كما رأينا كيف نفكر عندما نريد حل سؤال باستخدام الـ Recursion، كما قمنا بحل عدة أسئلة من خلالها رأينا نمط يتكرر باستمرار في الحل وهو أن نبدأ بالتفكير في كيفية جعل الـ input أصغر للحصول على subproblems ثم نقوم بالتفكير في كيفية استخدام نتيجة تطبيق الدالة على الـ subproblems لحل السؤال الأصلي، ثم نقوم بالتفكير في الـ base case. شئ مهم في الـ Recursion عند كتابة الكود هو أن تفكر بشكل declarative بمعنى أن تفكر دائماََ في الوظيفة التي يجب أن تؤديها الدالة وأن تفترض أنها تؤدي هذه الوظيفة بنجاح على أي subproblem وهذا سيسهل عليك كتابة الكود.
المصادر


















Discussion