مقدمة 

هذا المقال هو الجزء الثاني من مقال making sense of recursion، بعدما رأينا كيفية عمل الـ recursion وكيفية استخدامه، في هذا المقال سنبني على ما تعلمناه في المقال السابق لنتعلم مبادئ جديدة وسنرى نوعية المشاكل التي يساعدنا الـ recursion على حلها.  

أغلب الأسئلة التي قمنا بحلها في المقال السابق كان يمكن حلها ببساطة باستخدام Loop دون الحاجة إلى استخدام recursion فعلى سبيل المثال سؤال مجموع الأعداد الصحيحة من 1 إلى N يمكن حله باستخدام loop كالتالي:

def s(n):
  result = 0
  for i in range(n + 1):
    result += i
  return res

حتى إذا كنت تفهم الـ recursion جيداََ فعلى الأرجح هذا الحل هو ما ستفكر فيه عند قراءة السؤال. وهذه إحدى المشاكل التي قد تواجهك أثناء تعلم الـ recursion وهي أنك في البداية ترى استخدام الـ recursion لحل أسئلة يمكن حلها بسهولة باستخدام Loop وهذا ما قد يجعلك تتسائل عن أهمية الـ recursion أو الفائدة من تعلمه. 

في هذا المقال، سنرى أمثلة متنوعة تظهر أهمية الـ recursion كأداة قوية لحل المشاكل.

Divide and conquer

أبرز الحالات التي يكون فيها الـ recursion مفيداََ هي خوارزميات divide and conquer

divide and conquer هو أحد أشهر الطرق لتصميم الخوارزميات والذي يعتمد على الـ recursion، باستخدام divide and conquer يمكننا حل العديد من المشاكل الصعبة بسهولة، وكمية الكود التي تكتبها عادة ما تكون صغيرةََ ويمكنك فهم ما الذي يقوم به الكود بمجرد قراءته، والميزة الأهم هي أنه يمكننا فعل كل ذلك بكفاءة

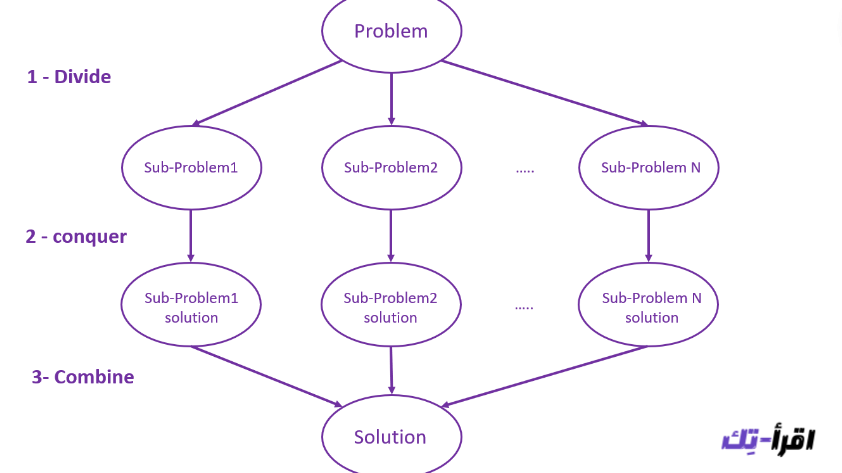
divide and conquer يتضمن ثلاث خطوات:

1. divide: 

تقسيم المشكلة الأصلية إلى مشاكل أصغر (subproblems)  

2. conquer:

حل كل subproblem على حدة، هذه هي الخطوة التي نقوم فيها باستخدام الـ recursion

3. combine:

استخدام حلول الـ subproblems للوصول إلى حل المشكلة الأصلية.

قد تتسائل الآن:  ما هو الفرق بين divide and conquer والـ recursion ففي المقال السابق ذكرنا أن الـ recursion يقوم بتقسيم المشكلة الأصلية إلى subproblems ثم يقوم بحل الـ subproblems للوصول إلى حل المشكلة الأصلية؟ 

الـ recursion مفهوم أوسع يشير إلى طريقة للبرمجة حيث تستدعي الدالة نفسها على input أصغر وهو مفهوم عام ويمكن استخدامه بطرق مختلفة. بينما divide and conquer طريقة تصميم خوارزميات تستخدم الـ recursion بطريقة معينة ففي الخطوة الأولى ( divide ) التي نقوم فيها بتقسيم المشكلة إلى subproblems فإن حجم كل subproblem عادةََ ما يكون حجم المشكلة الأصلية مقسوم على رقم فمثلاََ نقوم بتقسيم المشكلة الأصلية إلى نصفين أو إلى أربعة أرباع أو شئ مشابه لذلك، هذا بالنسبة لـ divide and conquer أما بالنسبة للـ recursion فلا يوجد طريقة محددة لتقسيم المشكلة الأصلية إلى subproblems. باختصار فإن كل divide and conquer يستخدم الـ recursion بينما ليس كل الـ recursion عبارة عن divide and conquer.

 لنفهم divide and conquer أكثر والفرق بينه وبين الـ recursion من خلال مثال، في هذا المثال مطلوب أن نقوم بكتابة دالة تأخذ array وتقوم بإيجاد أكبر رقم فيه، أمثلة:

• find_max([3, 8, 2, 5, 1, 7, 4, 6]) = 8
• find_max([-10, -5, -8, -3, -12]) = -3

لنتذكر الخطوات التي كنا نتبعها حتى نصل إلى الحل، أولاََ كيف يمكن جعل الـ input أصغر؟ يمكننا إزالة الرقم الأول من الـ array، ثانياََ كيف يمكن استخدام نتيجة استدعاء الدالة find_max على ما تبقى من الـ array بعد إزالة الرقم الأول لإيجاد أكبر رقم في الـ array؟ لنفترض أن الـ array المعطى هو [3,8,2,5] بعد إزالة الرقم الأول يصبح [8,2,5] واستدعاء الدالة find_max على هذا الـ array سيقوم بإيجاد أكبر رقم فيه وهو 8، نقوم بمقارنة 8 مع الرقم الذي قمنا بإزالته (3)  فنجد أن 8 أكبر وبالتالي 8 هو أكبر رقم في الـ array كله، إذا كان الـ array المعطى [9,8,2,5] سنقوم بإزالة 9 ثم نجد أكبر رقم في الـ array بعد إزالة 9 وهو 8 ثم نقوم بالمقارنة بينهم فنجد 9 أكبر وفي هذه الحالة 9 هو أكبر رقم في الـ array كله، باختصار ما نقوم به هو التالي:

1. إزالة أول رقم من الـ array. 
2. إيجاد أكبر رقم في ما تبقى من الـ array بعد إزالة أول رقم. 
3. نتيجة الدالة تكون العدد الأكبر بين أول رقم في الـ array المعطى و أكبر رقم في ما تبقى من الـ array بعد إزالة أول رقم.

def find_max(arr):
  # base case 1
  if len(arr) == 0:
    return None
  # base case 2
  if len(arr) == 1:
    return arr[0]

  # recursion
  max_from_1_to_end = find_max(arr[1:])
  return max(arr[0] , max_from_1_to_end)

حتى الآن لا يوجد جديد، استخدمنا الـ recursion بنفس الطريقة التي استخدمناها في المقال السابق، لنرى كيف يمكن حل نفس السؤال باستخدام divide and conquer.  

الفكرة في divide and conquer هي: بدلاََ من جعل الـ array أصغر عن طريق إزالة أول رقم، يمكننا جعله أصغر عن طريق تقسيمه إلى نصفين ( divide ) ثم نقوم باستدعاء الدالة find_max على النصفين لإيجاد الرقم الأكبر في كل نصف ( conquer ) ثم نقارن بين هذه الرقمين والنتيجة ستكون الرقم الأكبر بينهما ( combine ) كالتالي:

لتقسيم الـ array إلى نصفين نقوم بالتالي:

1. حساب قيمة الـ index عند منتصف الـ array والتي تساوي طول الـ array على 2 ونخزن هذه القيمة في متغير اسمه mid 
2. النصف الأول سيكون عبارة عن الأرقام من البداية ( index 0 ) وحتى المنتصف (index mid - 1 ) 
3. النصف الثاني سيكون عبارة عن الأرقام من بعد نهاية النصف الأول ( index mid ) وحتى نهاية الـ array. 

الكود لحل divide and conquer: